Tutorial 6: Time-Dependent DFT
- Author:
Tim Zuehlsdorff
- Date:
January 2016 (revised August 2023)
TDDFT in ONETEP
This tutorial aims at showing how to run a simple linear-response TDDFT calculation in ONETEP. Linear-response TDDFT is the main method of choice when computing optical excitations for large system sizes. In this formalism, excitation energies are directly obtained as the solutions to an effective eigenvalue equation. The approach implemented in ONETEP can be made to scale fully linearly with systems size, allowing for the computation of excitations in systems containing thousands of atoms.
In linear-response TDDFT, an excitation is expressed through a transition vector
that can be written in the basis of all possible Kohn-Sham transtions from
occupied to unoccupied states.
Thus unlike in standard ground state DFT, where a good representation of the
occupied KohnSham states is sufficient to obtain accurate results, in a TDDFT
calculation an equally good representation of a subset of the unoccupied
Kohn-Sham space is vital. Since the ONETEP support functions are optimised
in situ to ideally represent the occupied manifold, they generally provide a
relatively poor description of the unoccupied manifold, making them insufficient
for describing excitations in a linear-response framework. In practice, this
problem is removed by optimising a second set of support functions to ideally
span a low energy subset of the conduction space in a post-processing step after
a Singlepoint calculation. Together, the two sets of support functions form
an ideal representation of any given low energy excitation, thus enabling
efficient and accurate TDDFT calculations in very large systems.
Setting up a TDDFT calculation in ONETEP
- A TDDFT calculation in ONETEP thus proceeds in three separate steps:
A standard ground state calculation using
Task: Singlepoint. The code will write out.dknand.tightbox_ngwfsfiles containing the valence density kernel and the NGWF support functions.A conduction optimisation using
Task: Cond. The code will read in the converged.dknand.tightbox_ngwfsfiles from the ground-state optimisation and perform a postprocessingconduction optimisationof some low energy part of the conduction space manifold. It will write out.dkn_condand.tightbox_ngwfs_condfiles containing an effective density kernel for the low energy conduction space, as well as the NGWF support functions for the conduction space.A TDDFT calculation using
Task: Lr_tddft. The code will read in the density kernels and support functions for both the ground state and the conduction space calculations and then calculate the lowest n excitations of the system, where n is determined by the keywordlr_tddft_num_states.
In practice, it is possible to string these tasks together using
Task: Singlepoint Cond Lr_tddft in an input file that lists appropriate
keywords for all three calculation types. The tasks will be performed one after
another, without the user having to restart the calculation in between.
An NN-substituted nanoribbon
We turn to a simple example of an excited state calculation in a periodic system, namely that of an infinitely long graphene nanoribbon with two nitrogen substitutions. We will aim to compute excited states that are associated with the substitution and that are thus relatively localised in character. In a first step, we aim to build an input file for a pristine graphene nanoribbon in periodic boundary conditions. A primitive unit cell for the nanoribbon in question can be found below:
%block positions_abs
C 10.90 10.0 0.000
C 13.58 10.0 0.000
H 7.50 10.0 2.327
C 9.56 10.0 2.327
C 14.93 10.0 2.327
H 16.99 10.0 2.327
%endblock positions_abs
To generate an appropriate input file, copy the above primitive unit cell block
into a new input file called ribbon.dat.
ONETEP does not make use of any k-point sampling and all calculations are
effectively done at the \(\Gamma\)-point. Therefore, in order to accurately
simulate periodic structures it is necessary to simulate supercells rather than
primitive cells as would be done in standard plane wave DFT codes.
An appropriate supercell from the above primitive cell can be created by
repeating the primitive cell 7 times along the z-axis, translating the
z-coordinates of the atoms by the lattice vector of the primitive unit cell.
The resulting supercell should contain 48 atoms in total.
Now create an appropriate %block lattice_cart for the system.
The length of the supercell is specified by the length of your primitive cell
and the number of repeats of that cell. However, the size of the unit cell in
the x and y direction is free to specify by the user. Since the ONETEP method
uses periodic boundary conditions in all three directions, it is necessary to
include enough vacuum in the x and y direction of the simulation cell to
prevent it from interacting with its periodic neighbours. In this case, about
20 \({a}_{0}\) of vacuum between any atoms of different periodic images is
a reasonable length.
Using the lessons learnt from previous tutorials add a %block species and
%block species_pot block to your input file.
Choose an appropriate NGWF radius (try 8 \({a}_{0}\)) and kinetic energy
cutoff (around 600 eV) for your calculation.
When choosing the NGWF radius, note that ONETEP will not allow you to pick an
NGWF diameter that is larger than the dimensions of your simulation cell, as this
would cause an NGWF to interact with its periodic image. Finally, perform a
singlepoint calculation of the system. You can add a keyword
do_properties: T to the input file.
This will trigger the code to perform a properties calculation, write out a file
.val_bands containing all Kohn-Sham energies and write cube files of
selected Kohn-Sham states around the band gap.
Conduction optimisation
Once the ground state calculation is finished, it is necessary to perform a
conduction optimisation.
First, set Task: Cond and add a new block %block species_cond to the
input file.
This block is made up in an identical way as %block species and specifies
the number of support functions and their radius in the conduction optimisation.
In many practical examples, it is often advisable to choose a larger NGWF radius
for the conduction optimisation than for the ground state calculation,
especially if one is interested in lightly bound states, as unoccupied Kohn-Sham
states tend to be more diffuse than occupied ones (try 10 \({a}_{0}\)
for example).
A second keyword required for the conduction optimisation is the number of
conduction states that should be explicitly optimised (cond_num_states).
It is normally advisable to optimise only well-bound states as unbound states
are difficult to describe with localised orbitals. In order to do so, have a
look at the file .val_bands and count the number of Kohn-Sham states with
negative energy that are unoccupied. Note that cond_num_states expects the
number of electrons to be optimised as an input, thus in order to optimise the
five lowest unoccupied Kohn-Sham states in a spin-degenerate system, one should
choose cond_num_states: 10.
Once you have run the calculation, have a look at the output. You will find that ONETEP has generated a number of files such as cube files of unoccupied Kohn-Sham states expressed in terms of the optimised conduction NGWFs.
TDDFT calculation
We can now perform a full ONETEP TDDFT calculation of the system at hand.
To do so, set Task: Lr_tddft in the input file. Furthermore, add the
keywords lr_tddft_num_states: 6, lr_tddft_write_densities: T and
lr_tddft_analysis: T. The code will compute the lowest 8 singlet excitations
of the system and generate cube files for the electron, hole and transition
density for each excitation that can be visualised. Furthermore
lr_tddft_analysis: T triggers a breakdown of the converged TDDFT
eigenvectors into Kohn-Sham transitions, allowing you to study which are the
dominant transitions for each excitations.
Once you have performed the TDDFT calculation, look at the output file. You will see that the excitation energies and oscillator strengths for each of the excitations are printed out, as well as a detailed breakdown of excitation energies into Kohn-Sham transtions. Have a look at some of the cube files produced. Where are the excitations located in the system?
Nitrogen substitution
We can now move on from the case of the pristine nanoribbon to one with two
nitrogen substitutions.
For this purpose, copy the input file ribbon.dat to a new file
ribbon_NN.dat. In that file, remove two C-H from the
%block positions_abs that are opposite to each other in the ribbon,
and replace them by two N at the same positions where the C were located.
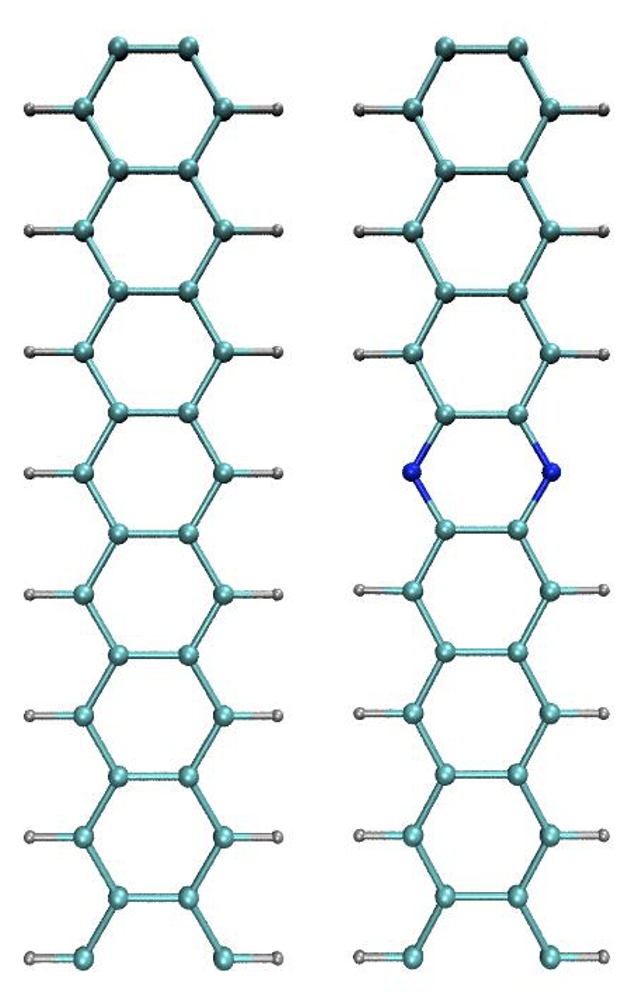
Fig. 3 Left: Pristine nanoribbon. Right: Nanoribbon with two carbons and two hydrogens substituted for two nitrogens
Note that in order to run the calculation, you will have to add the nitrogen
species to the %block species_pot, %block species and
%block species_cond blocks.
Change the task to Task: Singlepoint Cond Lr_tddft.
The code will run a ground state and conduction optimisation, followed by a
TDDFT calculation for the full system.
Have a look at the output. How do the excited states change due to the nitrogen
substitutions?
Where is each excited state located within the system?
Additional tasks
Substituting nitrogen atoms in the same place as carbon atoms does not yield a relaxed ground state structure, as the N-C bond is not of the same length as the C-C bond. Thus in order to obtain more realistic results for the substituted system, perform a geometry optimisation (see tutorial 4), followed by a ground state, conduction and TDDFT calculation of the full system. How do the results change? Furthermore, create a system where the nitrogen atoms are not substituted at exactly opposite positions in the structure, but an asymmetry along the z-axis is introduced. How does the character of the low energy excitations change?
Input files
All the files needed for the simulation can be downloaded from